This article comprises Chapter 3 of the book "Procedural Content Generation in Games: A Textbook and an Overview of Current Research" (edited by Noor Shaker, Julian Togelius and Mark J. Nelson). Information about the book, along with guidelines for citing it, can be found here. The text and images of the article have been adapted for online viewing; a few corrections have also been made.
This chapter addresses a specific type of game content, the dungeon, and a number of commonly used methods for generating such content. These methods are all "constructive", meaning that they run in fixed (usually short) time, and do not evaluate their output in order to re-generate it. Most of these methods are also relatively simple to implement. And while dungeons, or dungeon-like environments, occur in a very large number of games, these methods can often be made to work for other types of content as well. We finish the chapter by talking about some constructive generation methods for Super Mario Bros. levels.
Contents
Introduction
A dungeon, in the real world, is a cold, dark and dreadful place where prisoners are kept. A dungeon, in a computer game, is a labyrinthine environment where adventurers enter at one point, collect treasures, evade or slay monsters, rescue noble people, fall into traps and ultimately exit at another point. This conception of dungeons probably originated with the roleplaying board game Dungeons & Dragons, and has been a key feature of almost every computer role playing game (RPG), including genre-defining games such as the Legend of Zelda series and the Final Fantasy series, and recent megahits such as The Elder Scrolls V: Skyrim. Of particular note is the "roguelike" genre of games which, following the original Rogue from 1980, features procedural runtime dungeon generation; the Diablo series is a high-profile series of games in this tradition. Because of this close relationship with such successful games, and also due to the unique control challenges in their design, dungeons are a particularly active and attractive PCG subject.
For the purposes of this chapter, we define adventure and RPG dungeon levels as labyrinthic environments, consisting mostly of inter-related challenges, rewards and puzzles, tightly paced in time and space to offer highly structured gameplay progressions [6]. An aspect which sets dungeons apart from other types of levels is a sophisticated notion of gameplay pacing and progression: although dungeon levels are open for free player exploration (more than e.g. platform levels), this exploration has a tight bond with the progression of challenges, rewards and puzzles, as intended by game designers. In contrast with e.g. platform levels or race tracks, dungeon levels encourage free exploration while keeping strict control over gameplay experience, progression and pacing (unlike open worlds, where the player is more independent). For example, players may freely choose their own dungeon path among different possible ones, but never encounter challenges that are impossible for their current skill level (since the space to back track is not as open as, for example, a sandbox city). Designing dungeons is thus a sophisticated exercise of emerging a complex game space from predetermined desired gameplay, rather than the other way around.
In most adventure games and RPGs, dungeons structurally consist of several rooms connected by hallways. While originally the term 'dungeon' refers to a labyrinth of prison cells, in games it may also refer to caves, caverns, or human-made structures. Beyond geometry and topology, dungeons include non-player-characters (e.g. monsters to slay, princesses to save), decorations (typically fantasy-based) and objects (e.g. treasures to loot). Procedural generation of dungeons refers to the generation of the topology, geometry and gameplay-related objects of this type of levels. A typical dungeon generation method consists of three elements:
- A representational model: an abstract, simplified representation of a dungeon, providing a simple overview of the final dungeon structure.
- A method for constructing that representational model.
- A method for creating the actual geometry of a dungeon from its representational model.
Above, we distinguished dungeons from platform levels. However, there are also clear similarities between these two types of game level. Platform game levels were made famous by classic games such as Super Mario Bros, Sonic, the Hedgehog, and their countless clones and near-clones, as well as by other games that have drawn inspiration from them; a modern-day example of a game in this tradition that features procedural level generation is Spelunky, discussed in the first chapter. Like dungeons, platform game levels typically feature free space, walls, treasures or other collectables, enemies and traps. However, in the game mechanics of platformers, the player agent is typically constrained by gravity: the agent can move left or right and fall down, but can typically only jump a small distance upwards. As a result, the interplay of platforms and gaps is an essential element in the vocabulary of platform game levels.
In this chapter, we will study a variety of methods for procedurally creating dungeons and platform game levels. Although these methods may be very disparate, they have one feature in common: they are all constructive, producing only one output instance per run, in contrast with e.g. search-based methods. They also have in common that they are fast; some were even successful in creating levels at runtime. In general, these methods provide (rather) limited control over the output and its properties.The degree of control provided is nowadays a very important characteristic of any procedural method. With 'control' we mean the set of options that a designer (or programmer) has in order to purposefully steer the level generation process, as well as the amount of effort that steering takes. Control also determines to which extent editing those options and parameters causes sensible output changes, i.e. the intuitive responsiveness of a generator. Proper control assures that a generator creates consistent results (e.g. playable levels), while maintaining both the set of desired properties and variability.
We will discuss several families of procedural techniques. For simplicity, each of these techniques will be presented in the context of a single content type, either dungeons or platform game levels. The first family of algorithms to be discussed in this chapter is space partitioning. Two different examples of how dungeons can be generated by space partitioning are given; the core idea is to recursively divide the available space in pieces and then connect them to form the dungeon. This is followed by a discussion on agent-based methods for generating dungeons, with the core idea that agents dig paths into a primeval mass of matter. The next family of algorithms to be introduced is cellular automata, which turn out to be a simple and fast means of generating structures such as cave-like dungeons. Generative grammars, yet another family of procedural methods, are discussed next, as they can naturally capture higher-level dungeon design aspects. We then turn our attention into several methods that were developed for generating platform levels, some of which are applicable to dungeons as well. The chapter ends with a discussion of the platform level generation methods implemented in the commercial game Spelunky and the open-source framework Infinite Mario Bros, and its recent offshoot InfiniTux. The lab exercise will have you implementing at least one method from the chapter using the InfiniTux API.
Space Partitioning for Dungeon Generation
True to its name, a space partitioning algorithm yields a space partition, i.e. a subdivision of a 2D or 3D space into disjoint subsets, so that any point in the space lies in exactly one of these subsets (also called cells). Space partitioning algorithms often operate hierarchically: each cell in a space partition is further subdivided by applying the same algorithm recursively. This allows space partitions to be arranged in a so-called space partitioning tree. Furthermore, such a tree data structure allows for fast geometric queries regarding any point within the space; this makes space partitioning trees particularly important for computer graphics, enabling, for example, efficient raycasting, frustum culling and collision detection.
The most popular method for space partitioning is binary space partitioning (BSP), which recursively divides a space into two subsets. Through binary space partitioning, the space can be represented as a binary tree, called a BSP tree. Different variants of BSP choose different splitting hyperplanes based on some specific rules. Such algorithms include quadtrees and octrees: a quadtree partitions a two-dimensional space into four quadrants and an octree partitions a three-dimensional space into eight octants. We will be using quadtrees on two-dimensional images as the simplest example, although the same principles apply for octrees, on 3D space, and for other types of stored data. While a quadtree's quadrants can have any rectangular shape, they are usually equal-sized squares. A quadtree with a depth of n can represent any binary image of 2n by 2n pixels, although the total number of tree nodes (and its depth) depend on the structure of the image. The root node represents the entire image, and its four children represent the top left, top right, bottom left and bottom right quadrants of the image. If the pixels within any quadrant have different colors, that quadrant is subdivided; the process is applied recursively until each leaf quadrant (regardless of size) contains only pixels of the same color.
An example quadtree partition of a binary image (0 shown as red, 1 as black). Large areas of a single color, such as those on the right edge of the image, are not further partitioned. The image is 16 by 16 pixels, so the quadtree has a depth of 4. While a fully expanded quadtree (with leaf nodes containing information about a single pixel) would have 256 leaf nodes, the large areas of a single color result in a quadtree with 94 leaf nodes. The first layers of the tree are shown at the bottom: the root node contains the entire image, with the four children ordered as: top left quadrant, top right quadrant, bottom left quadrant, bottom right quadrant (although other orderings are possible).
When space partitioning algorithms are used in 2D or 3D graphics, their purpose is typically to represent existing elements such as polygons or pixels rather than create new ones. However, the principle that space partitioning results in disjoint subsets with no overlapping areas is particularly suitable for creating rooms in a dungeon or, in general, distinct areas in a game level. Dungeon generation via BSP follows a macro approach, where the algorithm acts as an all-seeing dungeon architect rather than a 'blind' digger as is often the case with agent-based approaches presented here. The entire dungeon area is represented by the root node of the BSP tree and is partitioned recursively until a terminating condition is met (such as a minimum size for rooms). The BSP algorithm guarantees that no two rooms will be overlapping, and allows for a very 'structured' appearance of the dungeon.
How closely the generative algorithms follow the principles of 'traditional' partitioning algorithms affects the appearance of the dungeon created. For instance, a dungeon can be created from a quadtree by selecting quadrants at random and splitting them; once complete, each quadrant can be assigned a value of 0 (empty) or 1 (room), taking care that all rooms are connected. This creates very symmetric, 'square' dungeons such as those seen below. Furthermore, the principle that a leaf quadrant must consist of a uniform element (or of same color pixels, in the case of images) can be relaxed for the purposes of dungeon generation; if each leaf quadrant contains a single room but can also have empty areas allows for rooms of different sizes, as long as their dimensions are smaller than the quadrant's bounds. These rooms can then be connected with each other, using random or rule-based processes, without taking the quadtree into account at all. Even with this added stochasticity, dungeons are still likely to be very neatly ordered.
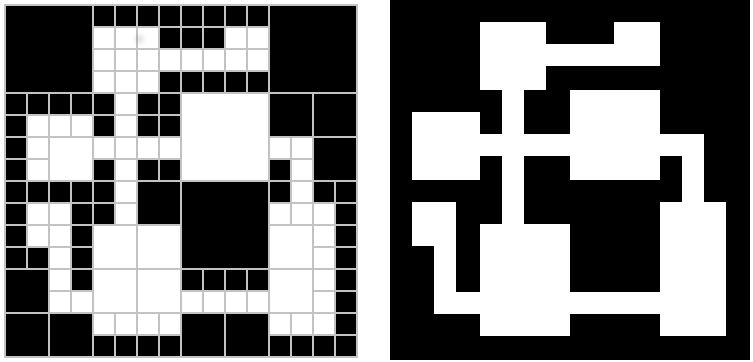
A dungeon created using a quadtree, with each cell consisting entirely of empty space (black) or rooms (white)
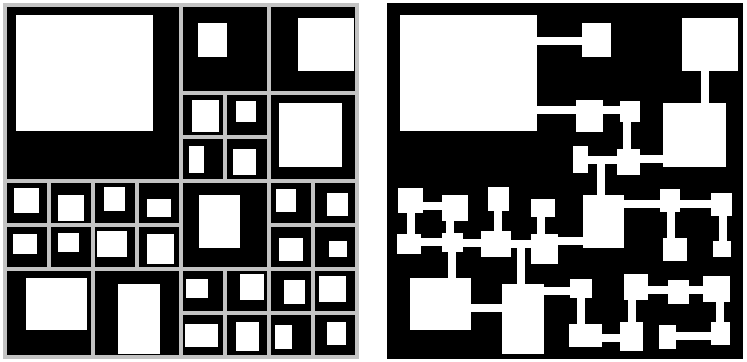
A dungeon created using a quadtree, but with each quadrant containing a single room (placed stochastically) and empty space; corridors are added after the partitioning process is complete.
We now describe an even more stochastic approach loosely based on BSP techniques. We consider an area for our dungeon, of width w and height h, stored in the root node of a BSP tree. Space can be partitioned along vertical or horizontal lines, and the resulting partition cells do not need to be of equal size. While generating the tree, in every iteration a leaf node is chosen at random and split along a randomly chosen vertical or horizontal line. A leaf node is not split any further if it is below a minimum size (we will consider a minimal width of w=4 and minimal height of h=4 for this example). In the end, each partition cell contains a single room; the corners of each room are chosen stochastically so that the room lies within the partition and has an acceptable size (i.e. is not too small). Once the tree is generated, corridors are generated by connecting children of the same parent with each other. Below is the high-level pseudo-code of the generative algorithm, and the image below shows the process of generating a sample dungeon.
1: start with the entire dungeon area (root node of the BSP tree)
2: divide the area along a horizontal or vertical line
3: select one of the two new partition cells
4: if this cell is bigger than the minimal acceptable size:
5: go to step 2 (using this cell as the area to be divided)
6: select the other partition cell, and go to step 4
7: for every partition cell:
8: create a room within the cell by randomly choosing two points (top left and bottom right) within its boundaries
9: starting from the lowest layers, draw corridors to connect rooms in the nodes of the BSP tree with children of the same parent
10: repeat 9 until the children of the root node are connected

Visualization of the stochastic partition of a dungeon area A, which is contained in the root node of the BSP tree: A is split into B and C via a vertical line (its x-coordinate is determined randomly). The leaves are iteratively split further as long as they are above a specific size. After the tree is created, rooms and corridors are placed: for each leaf node in the BSP tree, a room is placed by randomly choosing coordinates for top left and bottom right corners, within the boundaries of the partition cell. Corridor connect nodes that share a parent.
While binary space partitioning was here primarily used to create non-overlapping rooms, it should be noted that the hierarchy of the BSP tree can be used for other aspects of dungeon generation as well. The image above has demonstrated how room connectivity can be determined by the BSP tree: using corridors to connect rooms belonging to the same parent reduces the chances of overlapping or intersecting corridors. Moreover, non-leaf partition cells can be used to define groups of rooms following the same theme; for instance, a section of the dungeon may contain higher-level monsters, or monsters that are more vulnerable to magic. Coupled with corridor connectivity based on BSP tree hierarchy, these groups of rooms may have a single entrance from the rest of the dungeon; this allows such a room to be decorated as a prison or as an area with dimmer light, favoring players who excel at stealthy gameplay.

The example dungeon of the above image, using the partitions to theme the room contents. Partition cells B and C are only connected by a single corridor; this allows the rooms of partition B to be locked away (green lock), requiring a key from cell C in order to be accessed (room L). Similarly, rooms of cell B contain only treasures and rewards, while rooms of partition C contain predominantly monsters. Moreover, the challenge rating of monsters in cell C is split between its child nodes: partition G contains weak goblins while cell F contains challenging monsters with magical powers. Further enhancements could increase the challenge of cell G by making it darker (placing fewer light sources), using different textures for the floor and walls of cell B, or changing the shape of rooms in cell C to circular.
Agent-based dungeon growing
Agent-based approaches for dungeon generation usually amount to using a single agent to dig tunnels and create rooms in a sequence. Contrary to the space partitioning approaches, an agent-based approach such as this follows a micro approach and is more likely to create an organic and perhaps chaotic dungeon instead of the neatly organized BSP dungeons. The appearance of the dungeon largely depends on the behavior of the agent: an agent with a high degree of stochasticity will result in very chaotic dungeons while an agent with some "look-ahead" may avoid intersecting corridors or rooms. It should be noted that the impact of the AI behavior's parameters on the generated dungeons' appearance is difficult to guess without extensive trial-and-error; as such, agent-based approaches are much more unpredictable than space partitioning methods. Moreover, there is no guarantee that an agent-based approach will create a dungeon without rooms overlapping with each other or a dungeon which spans only a corner of the dungeon area rather than its entirety. The following paragraphs will demonstrate two agent-based approaches for generating dungeons.

A short run of the stochastic, 'blind' digger. Already from this very short run, the agent has created a dead-end corridor and two overlapping rooms.
There is an infinite amount of AI behaviors for digger agents when creating dungeons, and they can result in vastly different results. As an example, we will first consider a highly stochastic, 'blind' method. The agent is considered to start at some point of the dungeon, and a random direction is chosen (up, down, left or right). The agent starts digging in that direction, and every dungeon tile dug is replaced with a 'corridor' tile. After making the first 'dig', there is a 5% chance that the agent will change direction (choosing a new, random direction) and another 5% chance that the agent will place a room of random size (in this example, between 3 and 7 tiles wide and long). For every tile that the agent moves in the same direction as the previous one, the chance of changing direction increases by 5%. For every tile that the agent moves without a room being added, the chance of adding a room increases by 5%. When the agent changes direction, the chance of changing direction again is reduced to 0%. When the agent adds a room, the chance of adding a room again is reduced to 0%. Below is the pseudo-code for running this algorithm.
1: initialize chance of changing direction Pc=5
2: initialize chance of adding room Pr=5
3: place the digger at a dungeon tile and randomize its direction
4: dig along that direction
5: roll a random number Nc between 0 and 100
6: if Nc below Pc:
7: randomize the agent's direction
8: set Pc=0
9: else:
10: set Pc=Pc+5
11: roll a random number Nr between 0 and 100
12: if Nr below Pr:
13: randomize room width and room height between 3 and 7
14: place room around current agent position
15: set Pr=0
16: else:
17: set Pr=Pr+5
18: if the dungeon is not large enough:
19: go to step 4

A short run of the informed, "look ahead" digger. In the end, the digger can't add a room or corridor that doesn't intersect with existing rooms and corridors, so generation is halted despite a large part of the dungeon area being empty.
In order to avoid the lack of control of the previous stochastic approach, which can result in overlapping rooms and dead-end corridors, the agent can be a bit more informed about the overall appearance of the dungeon and 'look ahead' whether the addition of a room would result in room-room or room-corridor intersections. Moreover, the change of direction does not need to be rolled in every step, to avoid winding pathways. We will consider a less stochastic agent with 'look ahead' as a second example. Like above, the agent starts at a random point in the dungeon. The agent checks whether adding a room in the current position will cause it to intersect existing rooms. If all possible rooms result in intersections, the agent picks a direction and a digging distance that will not result in the potential corridor intersecting with existing rooms or corridors. The algorithm stops if the agent stops at a location where no room and no corridor can be added without causing intersections. Below is the pseudo-code for running this algorithm.
1: place the digger at a dungeon tile
2: set helper variables Fr=0 and Fc=0
3: for all possible room sizes:
3: if a potential room will not intersect existing rooms:
4: place the room
5: Fr=1
6: break from for loop
7: for all possible corridors of any direction and length 3 to 7:
8: if a potential corridor will not intersect existing rooms:
9: place the corridor
10: Fc=1
11: break from for loop
12: if Fr=1 or Fc=1:
13: go to 2
The examples provided with the "blind" and "look-ahead" digger agents show naive, simple approaches; the images above show to a large degree 'worst-case scenarios' of the algorithm being run, with resulting dungeons being either overlapping or prematurely terminated. While simpler or more complex code additions to the provided digger behavior can avert many of these problems, the fact still remains that it is difficult to anticipate such problems without running the agent's algorithm on extensive trials. This may be a desirable attribute, as the uncontrollability of the algorithm may result in organic, realistic caves (simulating human miners trying to tunnel their way towards a gold vein) and reduce the dungeon's predictability to a player, but may also result in maps that are unplayable or unentertaining. More than most approaches presented in this chapter, the digger agent's parameters can have a very strong impact on the playability and entertainment value of the generated artefact and tweaking such parameters to best effect is not a straightforward or easy task.
Cellular Automata
A cellular automaton (plural: cellular automata) is a discrete computational model. Cellular automata are widely studied in computer science, physics and even some branches of biology, as models of computation, growth, development, physical phenomena, etc. While cellular automata have been the subject of many publications, the basic concepts are actually very simple and can be explained in a few paragraphs and a picture or two.
A cellular automaton consists of an n-dimensional grid, a set of states and a set of transition rule. Most cellular automata are either 1-dimensional (vectors) or 2-dimensional (matrices). Each cell can be in one of several states; in the simplest case, cells can be on or off. The distribution of cell states at the beginning of an experiment (at time t=0) is the initial state of the cellular automaton. From then on, the automaton evolves in discrete steps based on the rules of that particular automaton. At each time t, each cell decides its new state based on the state of itself and all of the cells in its neighborhood at time t-1.
The neighborhood defines which cells around a particular cell c affects c's future state. For one-dimensional cellular automata, the neighborhood is defined by its size, i.e. how many cells to the left or right the neighborhood stretches. For two-dimensional automata, the two most common types of neighborhoods are Moore neighborhoods and von Neumann neighborhoods. Both neighborhoods can have a size of any whole number, one or greater. A Moore neighborhood is a square: a Moore neighborhood of size 1 consists of the eight cells immediately surrounding c, including those surrounding it diagonally. A von Neumann neighborhood is like a cross centred on c: a von Neumann neighborhood of size 1 consists of the four cells surrounding c above, below, to the left and to the right.
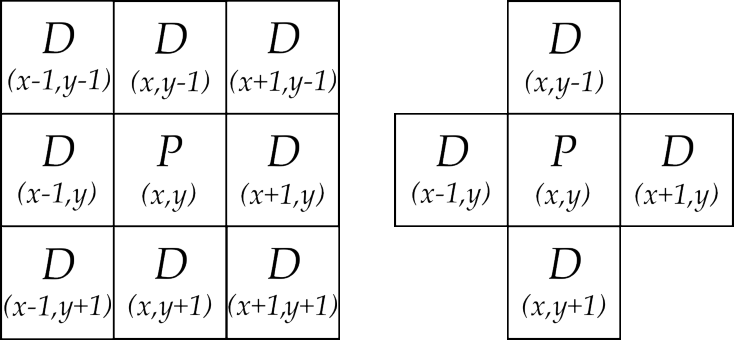
Moore neighborhood (left) and von Neumann neighborhood (right) for cellular automata.
The number of possible configurations of the neighbourhood equals the number of states for a cell to the power of the number of cells in the neighbourhood. These numbers can quickly become huge, for example a two-state automaton with a Moore neighbourhood of size two has 225=33554432 configurations. For small neighbourhoods, it is common to define the transition rules as a table, where each possible configuration of the neighbourhood is associated with one future state, but for large neighbourhoods the transition rules are usually based on the proportion of cells that are in each state.
Cellular automata are very versatile, and several types have been shown to be Turing complete. It has even been argued that they could form the basis for a new way of understanding nature through bottom-up modelling [19]. However, in this chapter we will mostly concern ourselves with how they can be used for procedural content generation.
In a paper from 2010, Johnson et al. describe a system for generating infinite cave-like dungeons using cellular automata [3]. The motivation was to create an infinite cave crawling game, with environments stretching out endlessly and seamlessly in every direction. An additional design constraint is that the caves are supposed to look organic or eroded, rather than having straight edges and angles. No storage medium is large enough to store a truly endless cave, so the content must be generated at runtime, as players choose to explore new areas. The game does not scroll but instead presents the environment one screen at a time, which offers a time window of a few hundred milliseconds to create a new room every time the player exits a room.
This method uses the following four parameters to control the map generation process:
- A percentage of rock cells (inaccessible area)
- The number of cellular automata generations
- A neighbourhood threshold value that defines a rock (
T=5) - The number of neighbourhood cells.
Each room is a 50x50 grid, where each cell can be in one of two states: empty or rock. Initially, the grid is empty. The generation of a single room works as follows.
- The grid is "sprinkled" with rocks: for each cell, there is probability
r(e.g. 0.5) that it is turned into rock. This results in a relatively uniform distribution of rock cells. - A cellular automaton is applied to the grid for
n(e.g. 2) steps. The single rule of this cellular automaton is that a cell turns into rock in the next time step if at leastT(e.g. 5) of its neighbours are rock, otherwise it will turn into free space. - For aesthetic reasons the rock cells that border on empty space are designated as "wall" cells, which are functionally rock cells but look different.
This simple procedure generates a surprisingly lifelike cave-room. The images below shows a comparison between a random map (sprinkled with rocks) and the results of a few iterations of the cellular automaton.
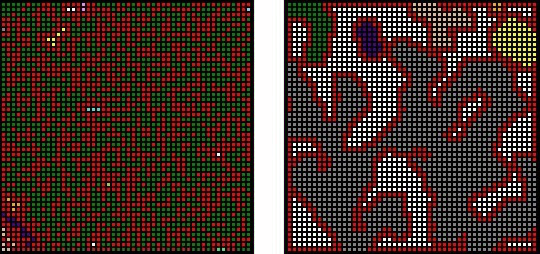
Cave generation: Comparison between a CA and a randomly generated map (r=0.5 in both maps); CA parameters: n=4, M=1, T=5. Rock and wall cells are represented by red and white color respectively. Colored areas represent different tunnels (floor clusters). Adapted from [3].
But while this generates a single room, the game requires a number of connected rooms. A generated room might not have any openings in the confining rocks, an there is no guarantee that any exits align with entrances to the adjacent rooms. Therefore, whenever a room is generated, its immediate neighbours are also generated. If there is no connection between the largest empty spaces in the two rooms, a tunnel is drilled between those areas at the point where they are least separated. Two more iterations of the cellular automaton are then run on all nine neighbouring rooms together, to smooth out any sharp edges. The image below shows the result of this process, in the form of nine rooms that seamlessly connect. This generation process is extremely fast, and can generate all nine rooms in less than a millisecond on a modern computer.

Cave generation: a 3x3 base grid map generated with CA. Rock and wall cells are represented by white and red colour respectively. Grey areas represent floor. (M=2;T=13;n=4;r=50%). Adapted from [3].
We can conclude that the small number of parameters, and the fact that they are relatively intuitive, is an asset of cellular automata approaches like Johnson et al.'s. However, this is also one of the downsides of the method: for both designers and programmers, it is not easy to fully understand the impact that a single parameter has on the generation process, since each parameter affects multiple features of the generated maps. It is not possible to create a map that has specific requirements, such as a given number of rooms with a certain connectivity. Therefore, gameplay features are somewhat disjoint from these control parameters. Any link between this generation method and gameplay features would have to be created through a process of trial and error.
Grammar-based dungeon generation
Generative grammars were originally developed to formally describe structures in natural language. These structures—phrases, sentences, etc. are modeled by a finite set of recursive rules that describe how larger-scale structures are built from smaller-scale ones, grounding out in individual words as the terminal symbols. They are generative because they describe linguistic structures in a way that also describes how to generate them: we can sample from a generative grammar to produce new sentences featuring the structures it describes. Similar techniques can be applied to other domains. For example, graph grammars [11] model the structure of graphs using a similar set of recursive rules, with individual graph nodes as the terminal symbols.
Back to our topic of dungeon generation, Adams [1] uses graph grammars to generate first-person shooter (FPS) levels. FPS levels may not obviously be the same as dungeons, but for our purposes his levels qualify as dungeons, because they share the same structure, a maze of interconnected rooms. He uses the rules of a graph grammar to generate a graph that describes a level's topology: nodes represent rooms, and an edge between two rooms means that they are adjacent. The method doesn't itself generate any further geometric details, such as room sizes. An advantage of this high-level, topological representation of a level is that graph generation can be controlled through parameters such as difficulty, fun, and global size. A search algorithm looks for levels that match input parameters by analyzing all results of a production rule at a given moment, and selecting the rule that best matches the specified targets.
One limit of Adams' work is the ad-hoc and hard-coded nature of its grammar rules, and especially the parameters. It is a sound approach for generating the topo- logical description of a dungeon, but generalizing it to a broader set of games and goals would require creating new input parameters and rules each time. Regardless, Adams' results showcase the motivation and importance of controlling dungeon generation through gameplay.
Dormans' work [2] used generative grammars to generate dungeon spaces for adventure games. Through a graph grammar, missions are first generated in the form of a directed graph, as a model of the sequential tasks that a player needs to perform. Subsequently, each mission is abstracted to a network of nodes and edges, which is then used by a shape grammar to generate a corresponding game space. This was the first method to successfully introduce gameplay-based control, most notably with the concept of a mission grammar. Still, the method does not offer real control parameters, since control is actually exerted by the different rules in the graph and shape grammars, which are far from intuitive for most designers.
Inspired by the work of Dormans, van der Linden et al. [5] proposed the use of gameplay grammars to generate dungeon levels. Game designers express a-priori design constraints using a gameplay-oriented vocabulary, consisting of player actions to perform in-game, their sequencing and composition, inter-relationships and associated content. These designer-authored constraints directly result in a generative graph grammar, a so-called gameplay grammar, and multiple grammars can be expressed through different sets of constraints. A grammar generates graphs of player actions, which subsequently determine layouts for dungeon levels. For each generated graph, specific content is synthesized by following the graph's constraints. Several proposed algorithms map the graph into the required game space and a second procedural method generates geometry for the rooms and hallways, as required by the graph.
This approach aims at improving gameplay-based control on a generic basis, as it provides designers with the tools to effectively create, from scratch, grammar-based generators of graphs of player actions. The approach is generic, in the sense that such tools are not connected to any domain, and player actions and related design constraints can be created and manipulated across different games. However, integration of graphs of player actions in an actual game requires a specialized genera- tor, able to transform such a graph into a specific dungeon level for that game. Van der Linden et al. demonstrated such a specialized generator for only one case study, yielding fully playable 3D dungeon levels for the game Dwarf Quest [18]. The images below shows a gameplay graph and a dungeon generated from this method.
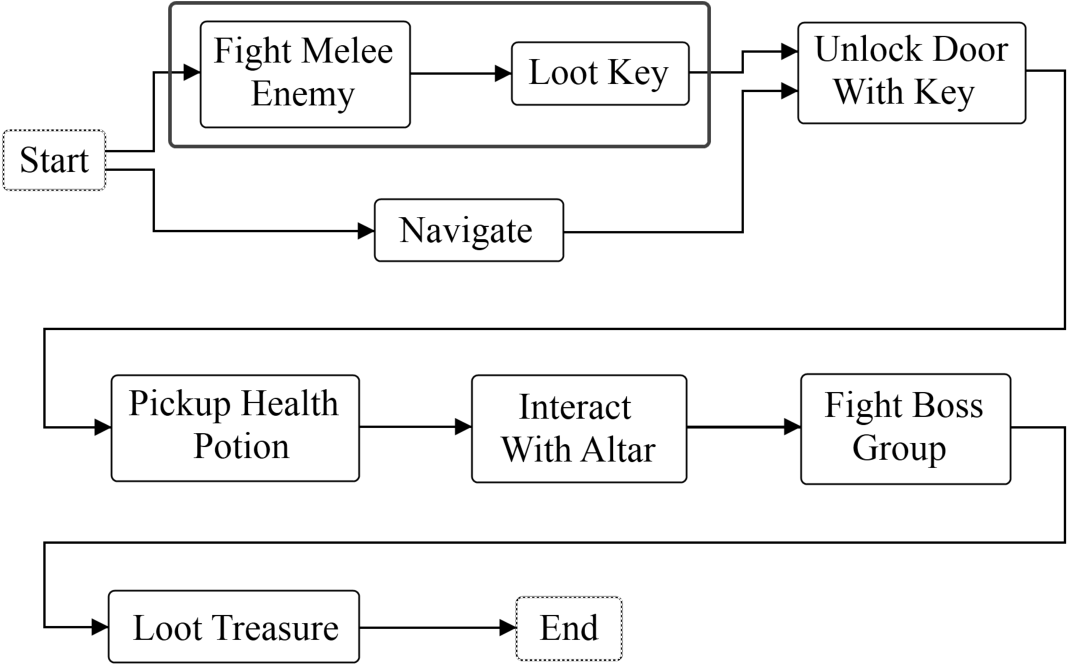
A gameplay graph (left) created by van der Linden et al. [11]

A corresponding Dwarf Quest layout (right) generated from the gameplay graph [11].
As for gameplay-based control, this approach empowers designers to specify and control dungeon generation with a more natural design-oriented vocabulary. Designers can create their own player actions and use them as the vocabulary to control and author the dungeon generator. For this, they specify the desired gameplay which then constrains game-space creation. Furthermore, designers can express their own parameters (e.g. difficulty), which control rule rewriting in the gameplay grammar. Setting such gameplay-based parameters allows for even more fine-grained control over generated dungeons.
Advanced platform generation methods
In this section, we turn our attention to platform generation methods, by discussing two recent methods that were originally proposed for generating platform levels. Unlike the previous sections, there is no single category or family to characterize these methods. Interestingly, as we will point out, the central concepts of each of them could very well contribute to improve the generation of dungeons as well.
The first method, proposed by Smith et al. [16], is rhythm-based platform generation. It proposes level generation based on the notion of rhythm, linked to the timing and repetition of user actions. They first generate small pieces of a level, called rhythm groups, using a two-layered grammar-based approach. In the first layer, a set of player actions is created, after which this set of actions is converted into corresponding geometry. Many levels are created by connecting rhythm groups, and a set of implemented critics selects the best level.
Smith et al. propose a set of 'knobs' that a designer can manipulate to control the generation process, including (i) a general path through the level (i.e. start, end, and intermediate line segments), (ii) the kinds of rhythms to be generated, (iii) the types and frequencies of geometry components, and (iv) the way collectables (coins) are divided over the level (e.g. coins per group, probability for coins above gaps, etc.). There are also some parameters per created rhythm group, such as the frequency of jumps per rhythm group, and how often specific geometry (springs) should occur for a jump. Another set of parameters provides control over the rhythm length, density, beat type, and beat pattern.
The large number of parameters at different levels of abstraction provides many control options, and allows for the versatile generation of very disparate levels. Furthermore, they relate quite seamlessly to gameplay, especially in the platformer genre. However, this approach could nicely tie in with dungeon generation as well. As with Dormans, a two-layered grammar is used, where the first layer considers gameplay (in this case, player actions) and the second game space (geometry). The notion of rhythm as defined by Smith et al. is not directly applicable to dungeons, but the pacing or tempo of going through rooms and hallways could be of similar value in dungeon-based games. The decomposition of a level into rhythm groups also connects very well with the possible division of a dungeon into dungeon-groups with distinct gameplay features such as pacing.
Our second method, proposed by Mawhorter et al. [8] is called Occupancy-Regulated Extension (ORE), and it directly aims at procedurally generating 2D platform levels. ORE is a general geometry assembly algorithm that supports human-design-based level authoring at arbitrary scales. This approach relies on pre-authored chunks of level as a basis, and then assembles a level using these chunks from a library. A chunk is referred to as level geometry, such as a single ground element, a combination of ground elements and objects, interact-able objects, etc. This differs from the rhythm groups introduced by Smith et al. [16], because rhythm groups are separately generated by a PCG method whilst the ORE chunks are pieces of manually created content in a library. The algorithm takes the following steps: (i) a random potential player location (occupancy) is chosen to position a chunk; (ii) a chunk is selected from a list of context-based compatible chunks; (iii) the new chunk is integrated with the existing geometry. This process continues until there are no potential player locations left, after which post-processing takes care of placing objects such as power-ups.
This framework is meant for general 2D platform games, so specific game elements and mechanics need to be filled in, and chunks need to be designed and added to a library. Versatile levels can only be generated given that a minimally interesting chunk library is used.
Mawhorter et al. do not mention specific control parameters for their ORE algorithm, but a designer still has some control. Firstly, the chunks in the library and their probability of occurrence are implicit parameters, i.e. they actually determine the level geometry and versatility, and possible player actions need to be defined and incorporated in the design of chunks. And above all, their mixed-initiative approach provides the largest amount of control one can offer, even from a gameplay-based perspective. However, taken too far, this approach could come too close to manually constructing a level, decreasing the benefits of PCG. In summary, much control can be provided by this method, but the generation process may still be not very efficient, as a lot of manual work seems to still be required for specific levels to be generated.
This ORE method proposes a mixed-initiative approach, where a designer has the option to place content before the algorithm takes over and generates the rest of the level. This approach seems very interesting also for dungeon generation, where an algorithm that can fill in partially designed levels would be of great value. Imagine a designer placing special event rooms and then having an algorithm add the other parts of the level that are more generic in nature. This mixed-initiative approach would increase both level versatility, and control for designers, while still taking work off their hands. Additionally, it would fit the principles of dungeon design, where special rooms are connected via more generic hallways. Also, using a chunk library fits well in the context of dungeon-level generation (e.g. combining sets of template rooms, junctions and hallways). However, 3D dungeon levels would typically require a much larger and more complex chunk library than 2D platform levels, which share a lot of similar ground geometry.
Example applications to platform generation
Spelunky
Spelunky is a 2D platform indie game originally created by Derek Yu in 2008 [20]. The PC version of the game is available for free. An updated version of the game was later released in 2012 for the Xbox Live Arcade with better graphics and more content. An enhanced edition was also released on PC in 2013. The gameplay in Spelunky consists of traversing the 2D levels, collecting items, killing enemies and finding your way to the end. To win the game, the player needs to have good skills in managing different types of resources such as ropes, bumps and money. Losing the game at any level requires the game to be restarted from the beginning.
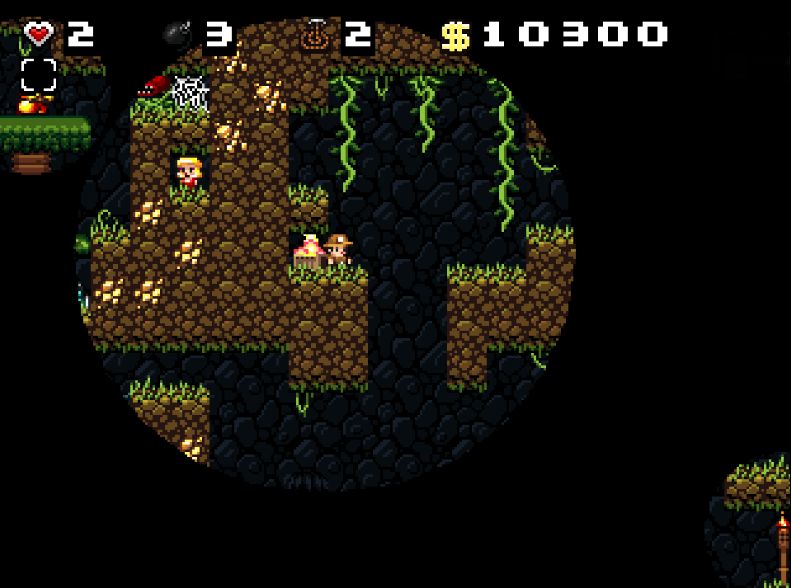
Snapshot from Spelunky [20].
Level generation in Spelunky. Adapted from [7].
Example room design in Spelunky. Adapted from [7].
The game consists of four groups of maps of increasing level of difficulty. Each set of levels has a distinguished layout and introduces new challenges and new types of enemies. An example level from the second set is presented in the image below. The standout feature of Spelunky is the procedural generation of game content. The use of PCG allows the generation of endless variations of content that are unique in every playthrough.
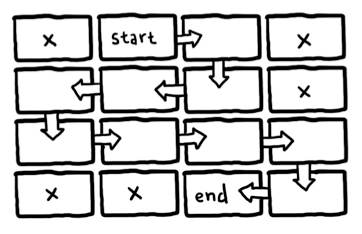
Each level in Spelunky is divided into a 4x4 grid of 16 rooms with two rooms marking the start and the end of the level (see the image below) and corridors connecting adjacent rooms. Not all the rooms are necessarily connected; in this image there are some isolated rooms such as the ones at the top left and bottom left corners. In order to reach these rooms, the player needs to use bombs, which are a limited resource, to destroy the walls.
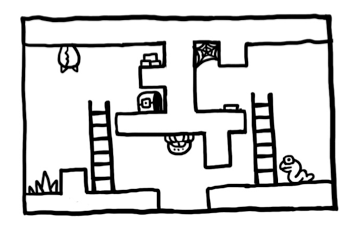
The layout of each room is selected from a set of predefined templates. To the left is an example template for one of the rooms. In each template, a number of chunks are marked in which randomisation can occur. Whenever a level is being generated, these chunks are replaced by different types of obstacle according to a set of randomized number generators [7]. Following this method, a new variation of the level can be generated with each run of the algorithm.
More specifically, each room in Spelunky consists of 80 tiles arranged in an 8x10 matrix [4]. An example room template can be:
0000000011
0060000L11
0000000L11
0000000L11
0000000L11
0000000011
0000000011
1111111111
Where 0 represents an empty cell, 1 stands for walls or bricks, L for ladders. The 6 in this example can be replaced by random obstacles permitting the generation of different variations. The obstacles, or traps, are usually of 5x3 blocks of tiles that overwrite the original tiles. Example traps included in the game can be spikes, webs or arrow traps, to name some.
While the basic layout of the level is partially random, with the presence of opportunities for variations, the placement of monsters and traps is 100% random. After generating the physical layout, the level map is scanned for potential places where monsters can be generated. These include, for example, a brick with empty tiles behind that offer enough space for generating a spider. There is another set of random numbers that controls the generation of monsters. These numbers control the type and the frequency of generation. For example, there is a 20% chance of creating a giant spider and once a spider is generated, this probability is set to 0 preventing the existence of more than one giant spider in a level.
In this sense, level generation in Spelunky can be seen as a composition of three main phases: in the first phase, the main layout of the level is generated by choosing the rooms from the templates available and defining the entrance and exit points. The second phase is obstacle generation, which can be thought of as an agent going through the level and placing obstacles in predefined spaces according to a set of heuristics. The final phase is the monster-generation phase, where another agent searches the level and places a monster when enough space is found and a set of conditions is satisfied.
Infinite Mario Bros.
Super Mario Bros. is a very popular 2D platform game developed by Nintendo and released in the mid 1980s [9]. A public domain clone of the game, named Infinite Mario Bros. (IMB) [10] was later published by Markus Persson. IMB features the art assets and general game mechanics of Super Mario Bros. but differs in level construction. IMB is playable on the web, where the Java source code is also available. While implementing most features of Super Mario Bros., the standout feature of IMB is the automatic generation of levels. Every time a new game is started, levels are randomly generated by traversing the level map and adding features according to certain heuristics.
The internal representation of levels in IMB is a two-dimensional array of game elements. In "small" state, Mario is one block wide and one block high. Each position in the array can be filled with a brick block, a coin, an enemy or nothing. The levels are generated by placing the game elements in the two-dimensional level map.
Different approaches can be followed to generate the levels for this game [12,14,15,17]. In the following we describe one possible approach.
The Probabilistic Multi-pass Generator (PMPG) was created by Ben Weber [15] as an entry for the level generation track of the Mario AI Championship [13]. The generator is agent-based and works by first creating the base level and then performing a number of passes through it. Level generation consists of six passes from left to right and adding one of the different types of game elements. Each pass is associated with a number of events (14 in total) that may occur according to predefined uniform probability distributions. These distributions are manually weighted and by tweaking these weights one can gain control over the frequency of different elements such as gaps, hills and enemies.
The six passes considered are:
- An initial pass that changes the basic structure of the level by changing the height of the ground and starting or ending a gap;
- the second pass adds the hills in the background;
- the third pass adds the static enemies such as pipes and cannons based on the basic platform generated;
- moving enemies such as koopas and goombas are added in the fourth pass;
- the fifth pass adds the unconnected horizontal blocks, and finally,
- the sixth pass places coins throughout the level.
Playability, or the existence of a path from the starting to the ending point, is guaranteed by imposing constraints on the items created and placed. For example, the width of generated gaps is limited by the maximum number of blocks that the player can jump over, and the height of pipes is limited to ensure that the player can pass through.
Summary
Constructive methods are commonly used for generating dungeons and levels in roguelike games and certain platformers, because such methods run in predictable, often short time. One family of such methods is based on binary space partitioning: recursively subdivide an area into ever smaller units, and then construct a dungeon by connecting these units in order. Another family of methods is based on agents that “dig out” a dungeon by traversing it in some way. While these methods originate in game development and might be seen as somewhat less principled, other methods for dungeon or level generation are applications of well-known computer-science techniques. Grammar-based methods, which are more extensively covered in Chapter 5, build dungeons by expanding from an axiom using production rules. Cellular automata are stochastic, iterative methods that can be used on their own or in combination with other methods to create smooth, organic-looking designs. Finally, several related methods work by going through a level in separate passes and adding content of different types according to simple rules with probabilities. Such methods have been used for the iconic roguelike platformer Spelunky and also for the Mario AI framework, but could easily be adapted to work for dungeons.
References
[1] Adams, D.: Automatic generation of dungeons for computer games (2002). B.Sc. thesis, University of Sheffield, UK.
[2] Dormans, J.: Adventures in level design: generating missions and spaces for action adventure games. In: PCG’10: Proceedings of the 2010 Workshop on Procedural Content Generation in Games. ACM (2010).
[3] Johnson, L., Yannakakis, G.N., Togelius, J.: Cellular automata for real-time generation of infinite cave levels. In: Proceedings of the 2010 Workshop on Procedural Content Generation in Games (2010).
[4] Kazemi, D.: Spelunky’s Procedural Space.
[5] Van der Linden, R., Lopes, R., Bidarra, R.: Designing procedurally generated levels. In: Proceedings of the the 2nd AIIDE Workshop on Artificial Intelligence in the Game Design Process, pp. 41–47 (2013).
[6] Van der Linden, R., Lopes, R., Bidarra, R.: Procedural generation of dungeons. IEEE Transactions on Computational Intelligence and AI in Games 6(1), 78–89 (2014).
[7] Make Games: The Full Spelunky on Spelunky.
[8] Mawhorter, P., Mateas, M.: Procedural level generation using occupancy-regulated extension. In: IEEE Symposium on Computational Intelligence and Games (CIG), pp. 351 –358 (2010).
[9] Nintendo Creative Department: (1985). Super Mario Bros., Nintendo.
[10] Persson, M.: Infinite Mario Bros.
[11] Rozenberg, G. (ed.): Handbook of Graph Grammars and Computing by Graph Transformation: Volume I. Foundations. World Scientific (1997).
[12] Shaker, N., Nicolau, M., Yannakakis, G. N., Togelius, J., O’Neill, M.: Evolving levels for Super Mario Bros. using grammatical evolution. In: IEEE Conference on Computational Intelligence and Games (CIG), pp. 304–311 (2012).
[13] Shaker, N., Togelius, J., Karakovskiy, S., Yannakakis, G.: Mario AI Championship.
[14] Shaker, N., Togelius, J., Yannakakis, G. N.: Towards automatic personalized content generation for platform games. In: Proceedings of the AAAI Conference on Artificial Intelligence and Interactive Digital Entertainment (AIIDE). AAAI (2010).
[15] Shaker, N., Togelius, J., Yannakakis, G.N., Weber, B., Shimizu, T., Hashiyama, T., Sorenson, N., Pasquier, P., Mawhorter, P., Takahashi, G., Smith, G., Baumgarten, R.: The 2010 Mario AI championship: Level generation track. IEEE Transactions on Computational Intelligence and Games pp. 332–347 (2011).
[16] Smith, G., Treanor, M., Whitehead, J., Mateas, M.: Rhythm-based level generation for 2D platformers. In: Proceedings of the 4th International Conference on Foundations of Digital Games, FDG 2009, pp. 175–182. ACM (2009).
[17] Sorenson, N., Pasquier, P.: Towards a generic framework for automated video game level creation. In: Proceedings of the European Conference on Applications of Evolutionary Computation (EvoApplications), pp. 131–140. Springer LNCS (2010).
[18] Wild Card: (2013). Dwarf Quest.
[19] Wolfram, S.: Cellular Automata and Complexity: Collected Papers, vol. 1. Addison-Wesley Reading (1994).
[20] Yu, D., Hull, A.: (2009). Spelunky.
This article comprises Chapter 3 of the book "Procedural Content Generation in Games: A Textbook and an Overview of Current Research" (edited by Noor Shaker, Julian Togelius and Mark J. Nelson). Information about the book, along with guidelines for citing it, can be found here. The text and images of the article have been adapted for online viewing; a few corrections have also been made.